https://www.acmicpc.net/problem/3042
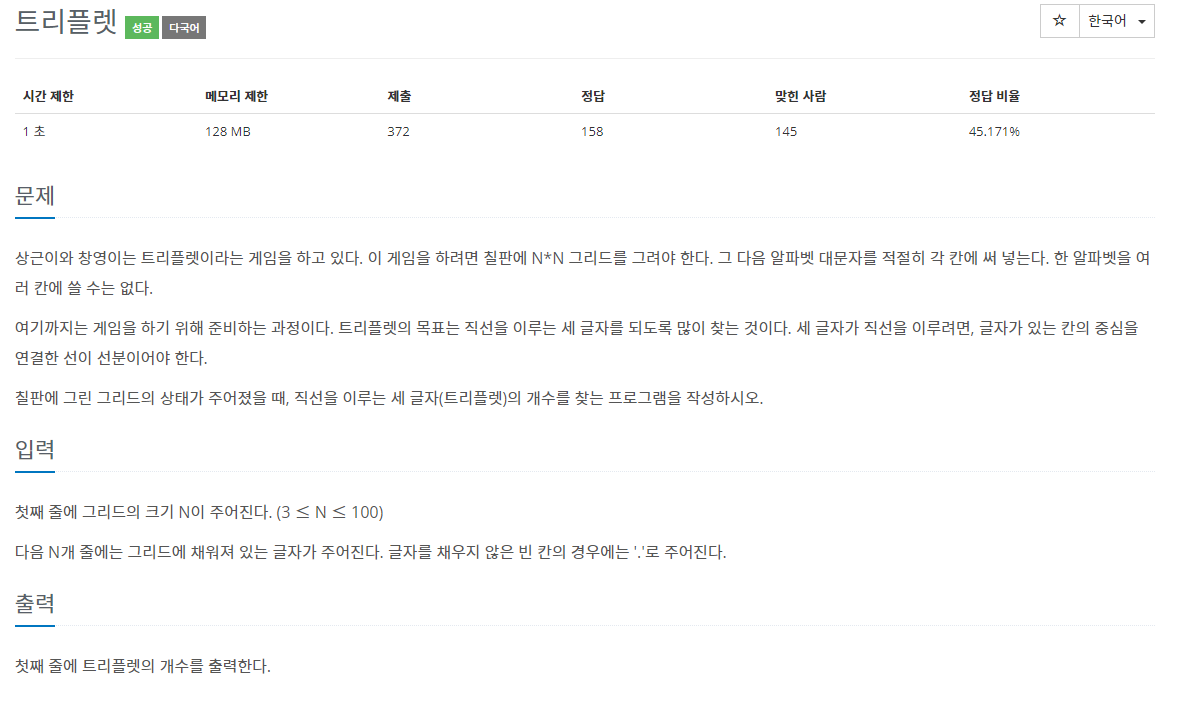
위와 같은 문제입니다.
처음에 문제를 봤을때 당황했었던 문제입니다. 문제는 N*N 격자 위에 있는 세 점이 같은 직선위에 있는 것을 트리플렛이라고 하는데 이의 개수를 찾는 문제였습니다. 제가 처음에 문제를 봤을때 점이 있을수 있는 위치는 N^2고 세점이므로 N^6이되니까 어떻게 풀지 막막했는데....
역시 문제를 잘봐야 한다고 문제에 알파벳을 여러칸에 쓸수 없으므로 최대 N*N격자 위에 26개의 점밖에 올라갈수 없었습니다. 그러면 시간복잡도가 26^3이 되고 완전탐색을 통해 해결할 수 있습니다.
이제 완전탐색중 고른 세 점이 같은직선위에 있는지 확인해야하는데 세 점을 각각 A,B,C라고 하고 각각의 좌표를 A(Ax,Ay) B(Bx,By) C(Cx,Cy) 라고 할때
선분AB의 기울기와 선분 BC의 기울기를 같을경우 같은 직선 위에 있다고 할 수 있습니다.
조건을 수식으로 나타내면

위처럼 나타낼수 있는데 프로그래밍에서 실수형 자료형의 연산 특히 두 실수형 자료형의 연산을 비교하는것은 매우 위험하므로 정수의 연산으로 바꾸는게 좋습니다.

로 나타낼수 있습니다.
아래는 풀이에 대한 C++코드입니다.
#include<stdio.h>
#include<vector>
#include<algorithm>
#include<iostream>
#include<string>
using namespace std;
char board[101][101];
vector<pair<int,int>> vec;
int gcd(int a,int b){
if(b==0) return a;
return gcd(b,a%b);
}
int main(){
int N;
int solve=0;
scanf("%i",&N);
for(int x=0;x<N;x++){
scanf("%s",&board[x]);
for(int y=0;y<N;y++){
if(board[x][y]!='.'){
vec.push_back({x,y});
}
}
}
sort(vec.begin(),vec.end());
for(int x=0;x<vec.size();x++){
for(int y=x+1;y<vec.size();y++){
for(int z=y+1;z<vec.size();z++){
int deltax1=vec[y].first-vec[x].first;
int deltay1=vec[y].second-vec[x].second;
int deltax2=vec[z].first-vec[y].first;
int deltay2=vec[z].second-vec[y].second;
int a=deltay1*deltax2;
int b=deltax1*deltay2;
if(a==b){
solve++;
}
}
}
}
printf("%i",solve);
}
'PS > boj' 카테고리의 다른 글
| 백준 22345 누적거리 (0) | 2022.06.27 |
|---|---|
| 백준 2616 소형기관차 (0) | 2022.06.26 |
| 백준 1594 전화번호 만들기 (0) | 2022.06.25 |
| 백준 14905 소수 4개의 합 (0) | 2022.06.24 |
| 백준 7347 플립과 시프트(C++) (0) | 2021.12.04 |
